简单信号处理

题目

物理知识告诉我们，对运动物体发射波，反射的波会受到多普勒效应的影响，造成反射波的频率的改变。而这一改变和物与发射源运动速度相关。这就是多普勒测速的基本原理。本题只需要处理出频率变化量。

简化实际情况，假设发射信号为$x(t)=A\cos(\omega_0 t+\phi)$，而接受信号接收到反射静止物体和运动物体的信号，为$y(t)=B\cos(\omega_0(t-t_0)+\phi)+D\cos(\omega_0(t-t_0)+\phi)$。而且为了方便，假定机器保留了原始的输出信号。

流程图

基本设计思路如下

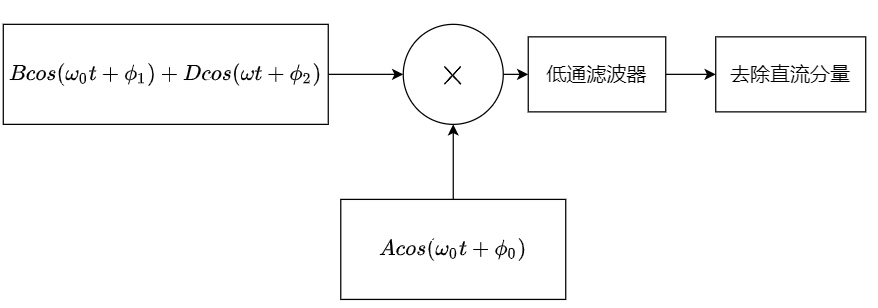
这个设计的基本思路是借鉴了双边带抑制载波调制的思路。借鉴自乘和滤波，获得低频的多普勒偏移频率。

数学证明

为了简化推导，接收的信号的时延，可以划归到相位变化中。即

$$ y(t)=B\cos(\omega_0t+\phi_1)+D\cos((\omega_0+\omega_d)t+\phi_2)\tag{1} $$

将信号和原始信号导入乘法器，得到

$$ x(t)*y(t)=\frac{AB}{2}(\cos(2\omega_0t+\phi_1)+\cos\phi_1)+\\ \frac{AD}{2}(\cos((2\omega_0+\omega_d)t+\phi_2)+\cos(\omega_d t+\phi_2)) \tag{2} $$

观察这个形式，很容易注意到，频率分量为$2\omega_0,2\omega_0+\omega_d,\omega_d,0$,分别是高频部分和低频部分。那么非常自然的想到，让信号通过一个低通滤波器即可。

$$ proc1(t)=\frac{AB}{2}\cos\phi_1+\frac{AD}{2}\cos(\omega_d t+\phi_2)\tag{3} $$

接下来想办法去除直流分量，就可以得到多普勒频率信号本身。由于实际上，我们是对离散量进行处理，那么去除直流量，可以简化成，求出信号在一段时间中离散值的平均数，减去即可。

$$ proc1(t).average()=\frac{AB}{2}\cos\phi_1\tag{4} $$

最后得到想要的信号。

$$ \begin{aligned} proc2(t)&=proc1(t)-proc1(t).average()\\ &=\frac{AD}{2}\cos(\omega_d t+\phi_2) \end{aligned}\tag{5} $$

实现细节

由于这是数字信号处理，所以不需要再加上专门的“去直流”。对离散值直接求平均减去即可。

滤波器采用 8 阶 Butterworth 低通滤波器。

结果

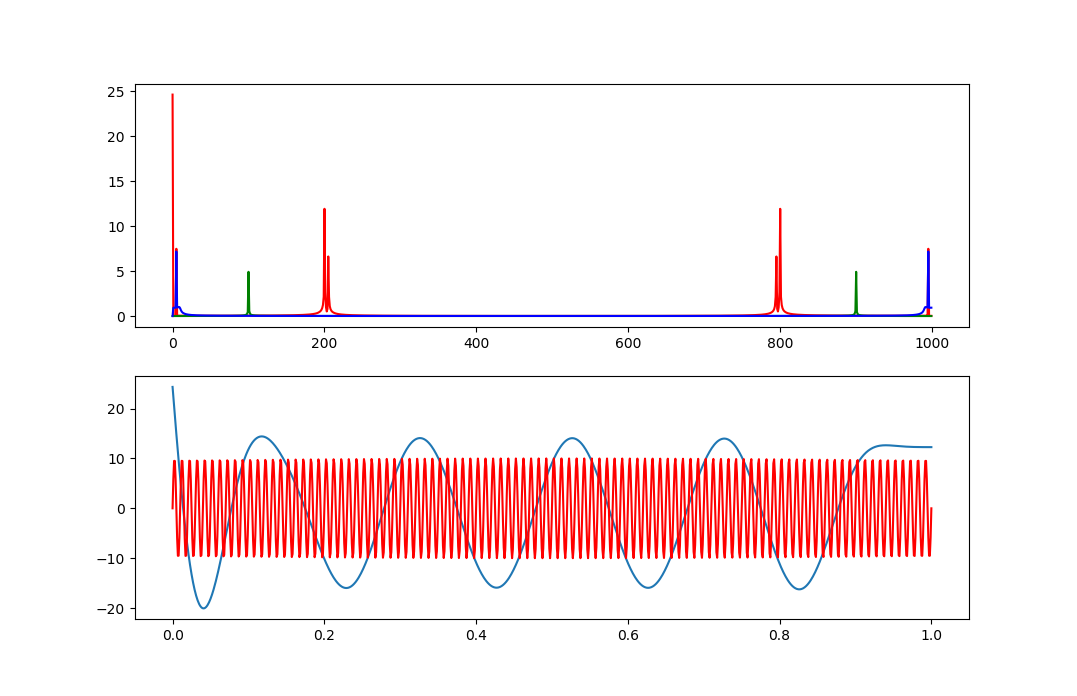
图一为频谱，红色为相乘信号，蓝色为输出信号。图二为时域。蓝色信号为输出，红色信号是初始发出的雷达信号，作为对比。

源代码

完整源代码如下。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
w = [100, 105]  #频率
a = [10, 5, 3]  #幅值
ph = [0, 1.4, 0.73]  #相位
N = 1000


#初始信号
def xtsig(t):
    return a[0] * np.sin(2 * np.pi * w[0] * t + ph[0])


#回波
def ytsig(t):
    return (a[1] * np.cos(2 * np.pi * w[0] * t + ph[1]) +
            a[2] * np.cos(2 * np.pi * w[1] * t + ph[2]))


def mul(t):
    return ytsig(t) * xtsig(t)


time = np.linspace(0, 1, N)

mulxy = mul(time)
x = xtsig(time)
#滤波
b, a = signal.butter(8, 0.02, 'lowpass')
low = signal.filtfilt(b, a, mulxy)
#去除直流分量
ave = np.average(low)
low = low - ave

f1 = np.fft.fft(mulxy)
absf1 = np.abs(f1) / N

f2 = np.fft.fft(x)
absf2 = np.abs(f2) / N

f3 = np.fft.fft(low)
absf3 = np.abs(f3) / N

plt.subplot(211)
p1, = plt.plot(np.arange(N), absf1, color='r')
p2, = plt.plot(np.arange(N), absf2, color='g')
p3, = plt.plot(np.arange(N), absf3, color='b')

plt.subplot(212)
p4, = plt.plot(time, low)
p5, = plt.plot(time, x, color='r')
plt.show()