王子游戏以及该游戏的不平衡性
规则
- 共有王子,公主和侍女(只能说真话的一边),皇后、女伯爵和侍卫(只能说假话的一边),男爵和牧师(可以任意选择说真假话)
- 大家除了王子互相知晓彼此身份,王子对其他人身份都不知道
- 王子需要向其他人每人问一个问题,再问完全员之后,可以选择任意一人再问一个问题。问题必须从下列 3 个中选择,回答必须按照上述身份的规则给出:
- 你的身份是什么
- 指定的某人身份是什么
- 公主是谁
- 问完所有问题,王子需要指定谁是公主,按下列情况结束游戏并判断胜负
- 王子指定的人是公主:王子、公主和侍女获胜
- 王子指定的人是皇后:皇后、女伯爵和侍卫获胜
- 王子指定的人既不是公主也不是皇后,而是其他任何身份:牧师和男爵获胜
理想条件
在好人优势更大的情况下:
- 可以无限次问问题
- 一个已知明牌的假话哥
注意其中的可以无限次问问题的条件。该条件下,每个人对局面看法都是已知的,而且真话哥没有别的选择,唯一的变化来自于假话哥和胡话哥的配合。如果假话哥和胡话哥之间配合,能保证了两边局面完全对称,两边胜率完全平分,可以认为这样的策略是两边都能接受的策略。
均衡的策略
3 组人分为 真话组、假话组、胡话组,组内部自称好侍女和公主。
明牌专说假话的人
- 称自己是胡话哥(确实为假)
- 说别人三个组都是逆顺序的侍女和公主(逆了顺序,一定为假话)
- 公主在任意一组自称侍女的位置(逆了顺序,一定为假话)
这样明牌说假话的人事实上王子从 ta 口中不能得到任何有用信息。
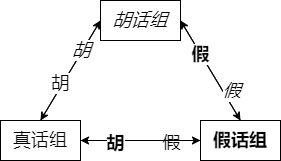
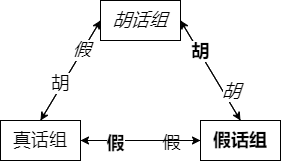
可能有以下两种可能性(胡话组用斜体,假话组是粗体)。第一种情况,胡话组和真话组对明牌假话人身份认同一致;第二种情况,胡话组和假话组对明牌假话人身份认同一致。两种情况对于王子绝对对称
- 两个互称胡话的组,对明牌假话人意见一致
- 两个互称胡话的组,对剩下那个组都认为是假话组,且次序一致
- 必有一个组被其他两组认为是胡话组,且次序相反:注意到第 2 种情况,假话组由于要说假话,对胡话组判断和真话组对胡话组判断次序相反;所以第 1 种情况,胡话组和假话组对真话组下判断时,注意次序相反就行
因此只有靠运气选组,也就是最后运气成分选到公主。
运气成分
概率计算不保证正确
已知上述 2 种情况,真话组
- 要么被 2 组同时认为是胡话且次序相反(此时被 2 组同时认为是假话的组是假话组)
- 要么被 2 组同时认为是假话(此时被 2 组同时认为是胡话的组是胡话组)
所以王子理论胜率也只有抛硬币的 $50\%$ ,其他两组分享 $25\%$ 。在不理想条件下,王子理论胜率应该更低。